Leetcode5: Longest Palindromic Substring(最长回文子串)

LeetCode:https://leetcode.com/problems/longest-palindromic-substring/

LeetCodeCn:https://leetcode-cn.com/problems/longest-palindromic-substring/

题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例

示例 1：
- 输入: “babad”
- 输出: “bab”
- 注意: “aba” 也是一个有效答案。
示例 2：
- 输入: “cbbd”
- 输出: “bb”

解题方法

感觉暴力法什么的,可以不再说了

中心扩展法

如果一个子串是回文,那么它本事是一个左右对称的形式,长度为n的子串,其中心有2n-1个,因为长度为偶数的子串,其中心可能在两个文字中间.接下来我们只要依次查找每个子串元素和两个元素中间作为回文子串的中心,记录其中最长的子串信息.

图解相关思路

在正式开始之前,我们先看一下如何查找一个中心能匹配的回文最长长度是如何得到的.

前面提到,奇数长度的回文串和偶数长度的回文串其中心是不同,在查找的过程中我们要分别区分两种情况来理解.

假设其长度为奇数,说明中心位置的元素无需和其它元素匹配(因为本身和本身一定相等),检测其左右相同长度的元素是否相等,如下图,假设中心位置是第1位的a,其左右元素相同,分别减少l和增加r,当时此时l = -1,并不合法,所以第1位作为中心的最长回文长度为3.

奇数中心

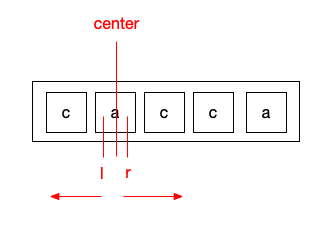
假设其长度为偶数,相当于其中心是一个空元素,也一定与本身相同,我们直接检测其两侧的元素是否相同,步骤同上.

偶数中心

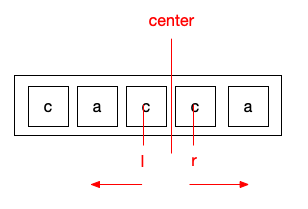
我们将”babab”作为参数,此时start(最长子串的开始位置)默认为0,end(最长子串的结束位置)默认为0.

输入条件

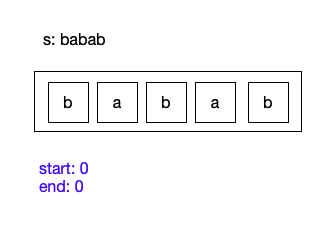
当我们搜索第0位时,len(奇) = 1, len(偶) = 0,其最大回文子串长度为1,大于当前start和end之间的差.我们需要更新statr和end的内容.end需要在i的基础上增加len/2,start需要在i的基础上减去(len - 1) /2,(防止偶数子串引起的越界问题).

i=0

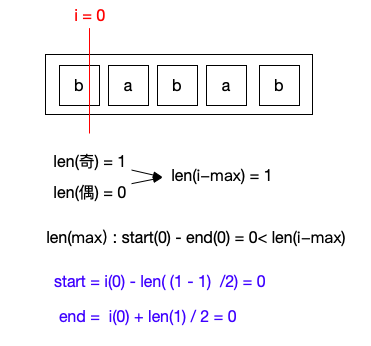
我们继续移动i,当i = 1时,此时其最长子串为3,更新start值为0,end值为2.

i=1

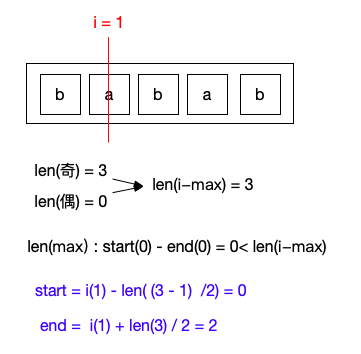
后边内容不重复, 因为每次计算相对来说都是独立,只需要将此为得到的最长回文子串长度和已知的比对即可

代码实现

public String longestPalindrome(String s) {
    if (s == null || s.length() < 1){
        return "";
    }
    int start = 0, end = 0;
    for (int i = 0; i < s.length(); i++) {
        int len = Math.max(isCenterNum(s, i , i), isCenterNum(s , i, i+1));
        if (len > end - start){
            start = i - (len - 1) / 2;
            end = i + len / 2;
        }
    }

    return s.substring(start, end + 1);
}

//计算某位中中心的最长回文子串方法
public int isCenterNum(String s, int l, int r){
    while (l >= 0 && r < s.length() && (s.charAt(l) == s.charAt(r))) {
        l--;
        r++;
    }
    return r - l - 1;
}